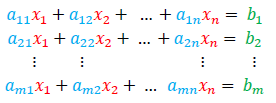En este tema se vera la representación de los sistemas de ecuaciones lineales por medio de una matriz; comúnmente se encuentran con problemas que se pueden representar mediante un sistema de ecuaciones lineales; por ejemplo, la cantidad de personas que camina por una calle bajo ciertas condiciones, como la hora, con o sin mascotas, comiendo o ejercitándose, etc. O bien, el número de ciertos contaminantes en el ambiente o en el agua, o la cantidad necesaria de ciertos átomos para crear una molécula determinada.
Una vez que un fenómeno, problema o situación sea modelado mediante un sistema de ecuaciones, su representación matricial es demasiado sencilla, tal y como se presenta en los siguientes subtemas.
3.1 Matriz principal y matriz ampliada.
3.1.1 Matriz principal.
Una matriz es principal o de coeficientes si resulta de la representación de un sistema de ecuaciones lineales; es decir, si A es la representación del sistema de ecuaciones, entonces A es una matriz principal o de coeficientes.
Se consideran los siguientes sistemas de ecuaciones:
Las siguiente matrices son ejemplos de las matrices principales de los sistemas dados.
A las matrices principales se les conoce con este nombre, debido a que a partir de ellas se encuentra la solución del sistema de ecuaciones del cual proviene.
Las matrices principales son las primeras matrices que se escriben con los coeficientes de las incógnitas de un sistema matricial; esto es, antes de sumarlas, restarlas o multiplicarlas por un escalar o por una matriz, ya que al realizar estas operaciones las matrices se modifican.
Todas las matrices descritas en el ejemplo anterior son matrices principales.
3.1.2 Matriz ampliada.
Se le conoce como matriz ampliada o aumentada a la combinación de dos matrices, una que representa a la matriz de los coeficientes de un grupo de ecuaciones y otra que representa a la matriz de constantes de las mismas ecuaciones.
Considerando el siguiente sistema de ecuaciones:
Se tienen las siguientes matrices:
Donde A es una matriz de coeficientes del sistema y B es una matriz de las constantes. Con estas matrices se puede construir la matriz aumentada (A|B), tal y como se muestra a continuación.
Las matrices aumentadas forman una parte muy importante dentro del estudio y en la mayoría de los casos son las que más se utilizan, ya que son las únicas que ofrecen un resultado sobre alguna situación planteada mediante un sistema matricial.
A partir de ahora, notaras que las incógnitas de tus ecuaciones son será x, y y z sino x1, x2, x3, …, xn.
3.2 Representación matricial de un sistema de ecuaciones lineales.
En este subtema se trabajarán los sistemas de ecuaciones lineales, para mostrar la manera en que estos se relacionan con las matrices. Suponiendo que se tiene un sistema de m ecuaciones lineales con n incógnitas, como el que se muestra a continuación:
De este sistema, se pueden extraer los coeficientes de las variables en cada una de las ecuaciones y con ellos se forma la matriz principal o de coeficientes, de la siguiente manera:
Se puede nombrar a un vector x que represente a las variables, y escribirlo como:
Y, por último, se escribe un vector b que represente a las constantes, las cuales son los segundos miembros de cada una de las ecuaciones que pertenecen al sistema de ecuaciones lineales:
Y con todos estos elementos, se puede representar al sistema de ecuaciones lineales por medio de matrices, como sigue.
O bien:
Cuando el sistema de ecuaciones lineales que se está representando es homogéneo, entonces, se sustituye el vector b por el vector 0 y el sistema de ecuaciones quedaría de la siguiente manera.
O bien:
Generalmente se tomará la matriz de coeficientes y la matriz o vector de constantes al representar sistemas de ecuaciones, ya que son los elementos que se necesitan para construir la matriz aumentada, la cual permitirá obtener o desarrollar algún resultado. Por ejemplo, se tiene el siguiente sistema de ecuaciones lineales:
Se representan los coeficientes por la siguiente matriz de 3x3
Y por la matriz de 3x1 a las constantes:
Se forma la matriz aumentada
O bien:
Esta es la matriz aumentada del sistema de ecuaciones lineales anterior.