Introducción:
En
esta actividad, tomando en cuenta los conocimientos que hasta el momento has
aprendido, se proponen ejercicios sobre producto escalar, condición de
perpendicularidad y producto cruz, recuerda que cada conocimiento aporta para la
resolución del problema prototípico planteado de la unidad.
Desarrollo:
1. Lee
con atención lo que se te solicita en cada punto y resuelve los ejercicios.
I. Encuentra
el ángulo que existe entre los siguientes pares de vectores.
a) u
= 2i – 4j, v = 3i + 2j
b) u
= 6i – 11j, v = 11i + 9j
c) u
= i + j, v = – 5i + 7j
d) u
= 5i – 4j, v = 3i + 4j
e) u
= 25i + 45j, v = 5i + 9j
f) u
= -13i -10j, v = 13i – 10j
II. Establece
si los siguientes pares de vectores son o no perpendiculares entre sí.
a) u
= (3,5), v = (-5, 3)
Si
es ortogonal o perpendicular entre sí.
b) u
= (8, -2), v = (-1, 4)
No
ortogonal o perpendicular entre si
c) u
= (0,4), v = (2, 0)
Si
es ortogonal o perpendicular entre si
d) u
= (6, 9), v = (2, -3)
No
es ortogonal o perpendicular entre si
e) u
= (5, 0), v= (-5, 0)
No
es ortogonal o perpendicular entre si
f) u
= (0, 11), v = (-3, 0)
Si
es ortogonal o perpendicular entre si
III. Calcula
el producto cruz de los siguientes vectores.
a) u
= i + j – k, v = 2i – 3j + 5k
a) u
= 3i – 4j + 5k, v = 6j + k – 5k
b) u
= 11i + 15k, v = 2i + 2j + 2 k
c) u
= j – 5k + i, v = 3k + 7i – 4j
d) v
= 2j + 5k – 4i, v = 100i + 200j + 300k
e) u
= 0.1i – 0.7j + 0.4k, v = 0.09i + 0.02j – 0.4k
Conclusión.
Esta actividad me permitió reafirmar mis
conocimientos sobre los vectores, aprendí a discernir diferentes problemáticas y
ordenamiento de vectores.
Aunque en ocasiones necesite apoyo por parte
de mi maestra con ciertas interrogantes que se me presentaron durante los
ejercicios, en cuanto logre despejar mis dudas, resolví con facilidad los
ejercicios.
Referencias
Ditutor. (s.f.). Obtenido de
https://www.ditutor.com/vectores/vectores_ortogonales.html
México, U. A.
(2018). Algebra Lineal. México. Obtenido de
https://documentcloud.adobe.com/link/track?uri=urn%3Aaaid%3Ascds%3AUS%3A718c174d-05a9-4b5c-a541-ad2460de1a0a
Vitutor. (s.f.). Obtenido de
https://www.vitutor.com/geo/vec/b_7.html
Vitutor. (s.f.). Obtenido de
https://www.vitutor.com/analitica/vectores/producto_vectorial.html



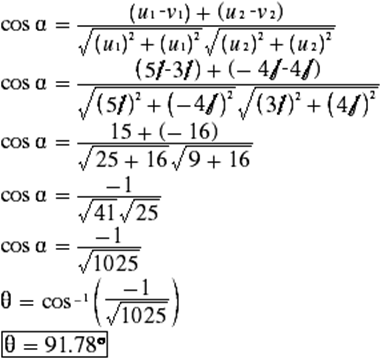

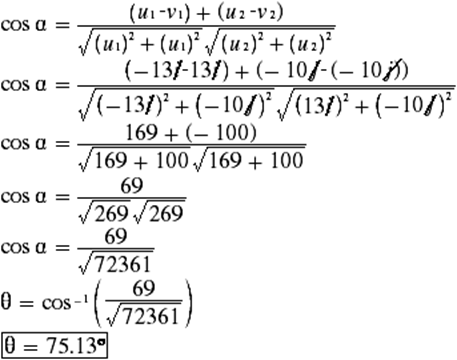






![clip_image002[4] clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgup7BRNE1Ps967eKhNkWvCvFrNREecUY8ZNqjwycsAs0JQlFbEpeAlNQ-bHvme5XrcKs6_YdWyvNj8dkdxv_07LVB8YBUcpcclyXjJEgkUtNLjayhM8IGFE24Xbz4znrv8ohpmoMWYdIiA/?imgmax=800)
![clip_image004[4] clip_image004[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjTo6Mjl-Faty8ff9P_TwG6Az8Di8nMZzvstfYRVjccINUhKeWSL3bkYYCgd-Z_jzu1JbsX3LBKsQjOmGny9I-gL8a0t4ovCxwHOoT8kdb8e0Pny_myifHj8pADKfvZ8QT1_gz-Yq8r3RPN/?imgmax=800)
![clip_image006[4] clip_image006[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgnq7PiJ_ow9EGEcnzFqd-2K_MgciCN-d7HKdxUAa_XRlT8OBSeqwFCmJUCtG_GbT4fTMacrMQ3LNer4U1kvT-22lMpVczW2vLNSRc8sE1qR6NlUANSh8nlg9ALa6Xt3Y8hw85qbMN3CjDr/?imgmax=800)
![clip_image008[4] clip_image008[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhiItDemqh8RweVjbh4HD51VDz45iByu7IOy7OqJACfdSM-cRyOf2JikAUWoe7JXxLKdV0iKo6S_hiANvKwjnBD-QeumDRD52NonN7gTPBAUBZKL_N71UFhZNnPkAtnm3OFYNUNA3teFGL0/?imgmax=800)
![clip_image010[4] clip_image010[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiiNrBNuykIWFqYwnU90JpfF8gyIegAC8E6ynKvTELu2oerPr32jGhnXiXkXVhjYNhJiI-50YY71bFt0hZ8pZLqXd06G5RoWOjHc2gvDZXYdaNeYzXoWiarSHP-4ziAhCusP9fwgKP1eDfg/?imgmax=800)
![clip_image012[4] clip_image012[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhg7z2xlxuMI0PeEkig-WBWibzwdDRUpUA1ULjMEKbWp1vs6bi1IGcWr3Wh8tyUnfqmvHagIY-5PQfLIVVVpgFgwfIaVfrSUJqQFCjEXJPg-_ywY3Sz6uSZzVmwLvz7-06o3vltcK4Pr1Pd/?imgmax=800)