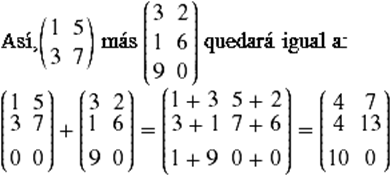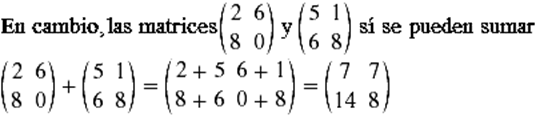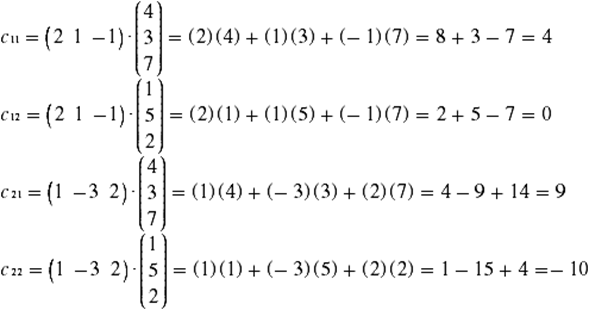¿Sabías que…?
Las hojas de cálculo, como las de Excel, son arreglos matriciales que ter permiten manipula datos numéricos. Habitualmente se utilizan para realizar bases de datos, informas, graficas estadísticas y clasificación de datos. Con ellas es posible hacer cálculos complejos con fórmulas y funciones y dibujar distintos tipos de graficas. Para ello, se utilizan operaciones entre celdas. Cada celda representa una entrada a la matriz.
Particularmente, Excel está compuesto por libros. Un libro es el archivo en que se trabaja y donde se almacenan los datos. Cada libro puede contener aproximadamente 250 hojas o carpetas. Cada hoja contiene aproximadamente 65,000 líneas y 256 columnas ordenadas numérica y alfabéticamente, respectivamente.
La variedad de aplicaciones de las matrices se presenta en tu alrededor, y bien es cierto que en todo momento las utilizas, también es cierto que con ellas realizas diferentes operaciones, sin darte cuenta.
Por ejemplo, en la situaciones más básicas, al realizar operaciones con los vectores, los cuales son matrices formadas por una columna o un renglón, al realizar la suma o resta de dos vectores columna o renglón, se están realizando operaciones con matrices.
Otras situaciones en las que se utilizan matrices más complejas, sería la comparación de precios. Si se requiere adquirir los útiles escolares y se compara la lista de precios en diferentes papelerías, se estaría haciendo una diferencia de precios en un arreglo rectangular lo cual es precisamente una resta de matrices.
Si se compran uniformes escolares para 2 niños de kínder y otros 2 niños de primaria, al realizar la suma de los precios, se estaría realizando una suma de matrices, ya que el uniforme se compone de calcetas, playera, short, pantalón. Si son 4 niños y todos van a la misma escuela y sus uniformes tienen el mismo precio, se realizaría el producto del costo de las partes que componen el uniforme por 4 que es la cantidad de niños; a esta operación se le conoce como el producto de una matriz por un escalar.
También se pueden encontrar aplicaciones más avanzadas. Por ejemplo, si estas realizando un estudio de contaminación en la ciudad, puede realizar una matriz en la cual se indiquen los diferentes contaminantes que te interesa estudiar y sus niveles de concentración por zona. O puedes tener una matriz por zona y sumarlas para determinar el índice del contaminante en toda la ciudad.
Si vas a analizar el comportamiento de una bacteria en diferentes ambientes, o bien, bajo modificaciones genéticas manipuladas, te conviene realizar una matriz en la cual conserves tus datos. Por ejemplo, el nivel de afección de la bacteria en diferentes organismos vivos de acuerdo con la temperatura del ambiente. O bien, el poder de infección de acuerdo con la manipulación de un gene u otro.
O si imaginas que deseas averiguar cómo producir un combustible a partir de diferentes elementos naturales, puedes realizar un arreglo matricial en el cual pondrás las diferentes cantidades de cada elemento y su efectividad.
Ahora conocerás las operaciones que se realizan con las matrices.
2.1 Suma y resta de matrices.
2.1.1 Suma de matrices.
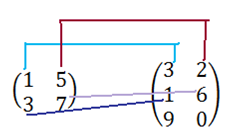
Sean A y B matrices de m x n; la suma de la matriz A y B es la matriz A+B, de m x n; en el gráfico se puede apreciar la manera en que se suman cada uno de los elementos.
Esto significa, que la matriz A+B de m x n se obtiene de sumas las componentes correspondientes de las matrices de m x n de A y B.
Se debe tener en cuenta que la suma entre dos matrices se puede realizar únicamente cuanto ambas matrices tienen el mismo número de elemento o bien el mismo tamaño.
Por ejemplo, las matrices:
Son incompatibles bajo la suma, puesto que, al intentar realizar la suma, se tendría:
Harían falta dos elementos, los cuales no posee las primera matriz; por lo tanto, no se pueden sumar.
Lo que se puede hacer en estos casos es aumentar en la matriz que sea más pequeña las filas o columnas necesarias para hacer ambas matrices de iguales dimensiones. Todos los elementos que se aumenten deberán ser iguales a cero.
2.1.2 Resta de matrices.
Sean A y B son matrices de m x n, la diferencia de A y B es una matriz de. M x n, A-B dada por
Esto significa, que la matriz A-B de m x n se obtiene de restar las componentes de B, de las respectivas componentes de A.
Al igual que para la suma de matrices, la diferencia se puede dar únicamente cuando las matrices que se están restando tienen el mismo número de elemento o bien que las matrices sean del mismo tamaño. Entonces las matrices
No pueden restarse, ya que son incompatibles debido a que tienen diferente número de filas, en cambio, las matrices
Si pueden restarse, puesto que tienen el mismo número de filas y de columnas, se resta la segunda de la primera se tiene:
Como en el caso de la suma, puedes hacer las matrices del mismo tamaño agregando ceros.
2.1.3 Propiedades de la suma y resta de matrices.
Sean A, B y C tres matrices de m x n, entonces se verifican las siguientes propiedades.
1. A+0=A, A-0=0
La suma o resta de una matriz con la matriz cero da como resultado la misma matriz, es decir que la matriz cero es el elemento neutro de la adición y sustracción de matrices.
2. A+B=B+A
La suma de matrices es conmutativa.
3. (A+B) +C=A+(B+C)
La suma de matrices es asociativa.
4. A+(-A) =0
Existe una matriz opuesta o el inverso aditivo de la matriz.
* las propiedades de la suma de matrices son similares a las propiedades de los números reales.
2.2 Producto de un escalar por una matriz.
En el tema anterior se presentaron las operaciones con matrices y se mencionó que estas se utilizan, por ejemplo, si se compran uniformes escolares y se componen de calcetas, playera, short, pantalón. Si son 4 niños y sus uniformes tienen el mismo precio, se realizaría el producto del costo de las partes que componen el uniforme por 4 que es la cantidad de niños.
Si, por ejemplo, sabes que el crecimiento de una cepa de bacterias es directamente proporcional a la temperatura del ambiente, entonces te servirá hacer una multiplicación de la matriz en donde tengas tus datos de crecimiento por bacteria, por un escalar que represente los grados de la temperatura.
Esta operación se le conoce como el producto de una matriz por una escalar. A continuación, se revisará de manera formal:
Entonces la matriz m x n, está dada por:
Es decir, que es la matriz que se obtiene al multiplicar cada componente de por . Observa el siguiente ejemplo.
Sea la matriz
Si se multiplica a la matriz por los escalares de 2 y 1/5 se tiene:
El producto de una matriz por un escalar aporta tres propiedades más, que se vinculan con las propiedades mencionadas en la suma y resta de matrices.
Sean A y B dos matrices y sean y dos escalares; entonces se verifican las siguientes propiedades.
· (+) = +
Propiedad distributiva del producto por un escalar.
· 1 =
El escalar 1 al multiplicarse por una matriz es la misma matriz.
· (+ ) = +
2.3 Producto matricial.
La multiplicación o producto matricial se realiza entre dos matrices o entre una matriz y un escalar, al igual que la multiplicación en aritmética. La multiplicación de matrices viene dada por un algoritmo, que permite calcular la multiplicación matricial, el cual es diferente del que se utiliza para multiplicar dos números. La diferencia es que la multiplicación de matrices no cumple con la propiedad conmutativa. A continuación, se conocerá la manera en que se realiza la multiplicación de matrices.
Se A una matriz de m x n y sea B una matriz de n x p. El producto de A y B es una matriz C=AxB de m x p, donde los elementos de c de C están determinados de la siguiente manera:
De este modo, cada elemento c de C queda determinado de manera única por el producto de un renglón de A con una columna de B.
Antes de realizar la multiplicación de matrices, se debe comprobar si están son compatibles bajo la multiplicación; para esto, el número de columnas debe de ser igual al número de filas de la segunda matriz, de lo contrario, el producto no se podrá realizar, ya que las matrices serian incompatibles bajo la multiplicación.
Ejemplo de producto de matrices.
Sean las matrices
Calcula su producto. A tiene 3 renglones y B tiene 3 columnas, de modo que dicha multiplicación de matrices puede realizarse.
El producto se determina de la siguiente manera.
Solución.
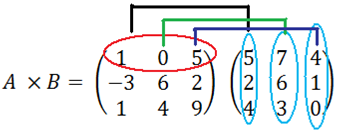
El primer paso para multiplicar dos matrices es tomar la primera fila de la matriz A y la primera columna de la matriz B, con estos dos vectores se realizará un producto escalar y el resultado será el elemento a11 de la nueva matriz y se continuará multiplicando la fila i por la columna j y el resultado será el elemento aij de la nueva matriz.
En el siguiente diagrama se ilustra la forma en que se multiplican dos matrices.
Entonces, se tiene que la matriz resultante del producto de las matrices A y B está dada por:
Se debe tener en cuenta que, si el número de filas de la primera matriz no coincide con el número de columnas de la segunda, entonces las matrices no se pueden multiplicar. Por esta misma razón, no es indispensable que las matrices sean cuadradas para se pueda efectuar su producto.
A continuación, se presenta el producto de dos matrices que no son cuadrada; para ser más precisos en este ejemplo se realizaran los productos por separado.
Ejemplo.
Sea la matriz A de 3x2 y la matriz B de 3x2, calcula su producto.
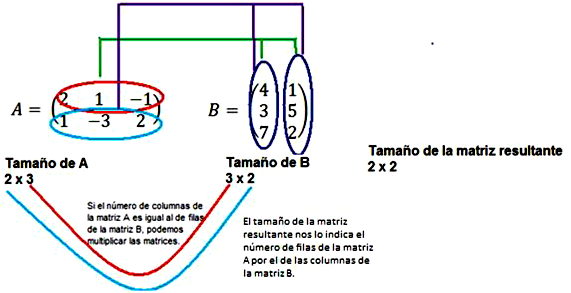
Debido a que las matrices no son cuadradas, primero se verifica si son o no compatibles bajo la multiplicación. Como la primera matriz es de 2x3 (dos filas, tres columnas) y la segunda es de 3x2 (tres filas, dos columnas), si se pueden multiplicar porque el número de columnas de A es igual al número de filas de B. Además, se puede identificar el tamaño de la matriz resultante tomando el número de filas de la primera matriz y el número de columnas de la segunda. De esta manera el resultado será una matriz cuadrada de 2x2; esto se resume mediante el siguiente esquema:
Ahora se realizará el producto de los elementos que se ilustran en el diagrama anterior:
Por lo tanto, se tiene que
Con esto se demuestra que, al multiplicar dos matrices, no es necesaria que estas sean cuadradas.
Un ejemplo de aplicación de las operaciones de matrices en investigación lo iras construyendo paso a paso en las siguientes secciones. Lo primero que debes hacer es representar los elementos de tu problema en forma matricial.