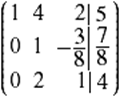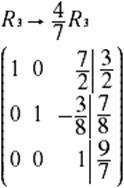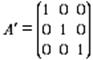Unidad 2. 4. Operaciones elementales de renglón.

Las operaciones elementales de renglón las utilizas en tu vida cotidiana, al modificar algunos hechos o acontecimientos que se pueden representar mediante un vector. Esto se ilustra con los siguientes ejemplos:

Si se tiene una lista de compras de alimentos perecederos y compras los mismos productos en las mismas cantidades cada semana, se puede encontrar la cantidad total que se comprar al mes, multiplicando el vector que las representa por el número de semanas que restan del mes que se encuentra en curso.

Imagina que está realizando un experimento en el cual analizas que sustancias se producen en diferentes reacciones químicas. Puedes hacer un arreglo matricial que exprese los compartimientos de tus sustancias. Supón que debes tener más presente una de las reacciones, entonces puedes intercambiar de lugar las filas de tu matriz y también puedes realizar otras interacciones entre los renglones para determinar si es posible obtener o no otra sustancia.

A continuación, se presenta de manera más específica cuales son las operaciones elementales de renglón, así como la manera en que estas se desarrollan. Por otra parte, se conocerán como obtener la matriz inversa mediante estas operaciones.

4.1        Aplicación de las operaciones elementales de renglón a una matriz.

De los cursos de álgebra que estudiaste en la secundaria y en el bachillerato conoces los sistemas de ecuaciones lineales. En ellos estudiaste que multiplicar o dividir ambos lados de una ecuación por un número distinto de cero dan una nueva ecuación, la cual es equivalente a la original.

Otras de las cosas que conoces de un sistema de ecuaciones es que, al sumar una ecuación, ya sea del sistema o equivalente a una de las del sistema, con otra del mismo sistema, se obtiene una ecuación que no la modifica y, además, si se intercambian de renglón dos ecuaciones de un mismo sistema, resulta un sistema equivalente al primero, es decir, que las soluciones serían las mismas.

Las operaciones elementales con renglones, aplicadas a la matriz aumentada, que representa un sistema de ecuaciones lineales, son las siguientes:

·         Multiplicar o dividir un renglón por un número diferente de cero.

·         Sumar un renglón original o su equivalente, con otro renglón.

·         Intercambiar dos renglones.

Cada una de las operaciones anteriores aplicadas sobre una matriz aumentada, no modifica la matriz, ya que forma una matriz equivalente a la primera. Por esto mismo, tampoco se altera el sistema de ecuaciones que dicha matriz representa.

El proceso de aplicar las operaciones elementales con renglones para simplificar una matriz aumentada se conoce como reducción de renglones.

Primero se pondrían en práctica las operaciones de renglones, para posteriormente ver como esto ayuda a resolver sistemas de ecuaciones lineales. Se va a desarrollar el siguiente ejemplo.

Sea

Una matriz aumentada; utiliza las operaciones elementales por renglón y encuentra la matriz identidad equivalente.

Para trabajar con los renglones y las columnas, se utilizará R_i para hacer referencia al renglón i, con esto se puede reducir la matriz de la siguiente manera.

Primero se escribe la matriz aumentada:

Para realizar las operaciones entre renglones, lo que conviene es realizar operaciones con los renglones de tal manera que en la diagonal principal queden unos. Como la matriz ya tiene al primer elemento de la diagonal igual a 1, se tiene que convertir a los elementos que se encuentran debajo de él, en ceros.

Paso 1.

−2₁+₂→₂ se multiplica al renglón 1, por -2 y se suma el renglón 2; el resultado de estas operaciones se va a colocar en el renglón 2, por lo que el renglón 1 permanecerá igual.

Este resultado lo puedes observar en el renglón 2 de la siguiente matriz.

Paso 2.

−₁+₃→₃ para que el elemento a₃₁ sea igual a cero, se multiplica al renglón 1 por -1 y se le suma el renglón 3, el resultado se va a colocar en el renglón 3, por lo que el renglón 1 pasara tal como está.

El resultado lo puedes observar en el renglón 3 de la siguientes matriz:

Paso 3.

−¹/₈₂→₂ se multiplica al renglón 2 por −¹/₈ para tener al 1 en la matriz principal.

El resultado quedaría tal como se muestra en la siguiente matriz:

Ya se tienen los tres unos en la matriz principal, falta hacer ceros a los demás elementos de la matriz de coeficientes; para ello, se realizan las siguientes operaciones:

Paso 4.

Al renglón 2 lo multiplicar por -4 y le sumas el renglón 1; al resultado lo colocas en el renglón 1.

Paso 5.

Al renglón 2 lo multiplicas por -2 y le sumas al renglón 3; el resultado lo colocas en el renglón 3. El renglón 2 pasa tal como está.

Como te podrás dar cuenta, las operaciones se realizaron de tal manera que el elemento a₁₂ y a₃₂ sean iguales a cero, pero el elemento a₃₃ de la diagonal principal en lugar de 1 es ⁷/₄; esto se resuelve fácilmente multiplicando ⁴/₇. El resultado se muestra en la siguiente matriz.

Paso 6.

Paso 7.

Paso 8.

La matriz aumentada que se obtuvo tiene unos en la diagonal principal y ceros en sus demás elementos, excepto en los que corresponden a las constantes. Entonces, sea llegado a la matriz identidad y sea conseguido con el uso de operaciones elementales de renglón.

Ahora se explica cómo las operaciones de renglón realizadas en la matriz asociada al sistema de ecuaciones ayudan en la solución de este.

Las matrices principales son aquellas que representan un sistema de ecuaciones lineales y que permiten obtener la solución de dicho sistema de forma muy sencilla. La manera para hacer esto, es la siguiente.

Como se estableció al principio, las operaciones con renglones forman nuevas matrices, las cuales son equivalentes a la matriz principal o bien a la matriz con la cual se comienza a trabajar; de esta manera se tiene la siguiente equivalencia.

Entonces, la nueva matriz de coeficientes equivalente a la matriz principal es una matriz identidad, denotada en este caso por A’ y así, se tiene que:

Por otra parte, la matriz o vector de constantes, que anteriormente era

Ahora es

Y, por último, quien no cambia es la matriz o vector de variables x.

El sistema solución lo puedes escribir tal y como se muestra a continuación:

O bien

De esta manera, si se desarrolla el producto escalar de las matrices del primer miembro, se tiene.

Sustituyendo el resultado en (1), se tiene

Por lo tanto, se tiene que

Estas son las soluciones de la matriz aumentada:

Se puede observar que el proceso de operaciones elementales de renglón de una matriz no es complicado, sino laborioso y dependiendo del tamaño de la matriz construida, puede llegar ser tedioso. Una manera más sencilla de obtener los valores de las variables es la siguiente:

Teniendo la matriz identidad en el lado izquierdo de la matriz aumentada, se igualan las variables correspondientes a cada posición, tal y como se muestra a continuación.

La matriz reducida por renglones queda de la siguiente manera:

A partir de ella, se pueden encontrar las soluciones, tomando en cuenta el orden de las variables; para esto, se asocia a la primera columna la variable x₁, a la segunda columna x₂ y la tercera columna x₃; de esta manera las soluciones son:

4.2        Matriz inversa mediante operaciones de renglón.

Se diría que la matriz inversa de una matriz cuadrada A_n es la matriz que cumple la siguiente propiedad:

Sean A y B dos matrices cuadradas; B es la matriz inversa de A si

 Es decir, si el producto matricial de A y B da como resultado a la matriz identidad, entonces B es la matriz inversa de A y se denota por A^-1; de esta manera, se puede escribir la ecuación anterior en términos de A como sigue:

A las matrices que tienen inversa se les llama invertibles. Las matrices cuadradas que no tienen inversa se conocen como matrices singulares. A su vez, también a las matrices invertibles se les conoce como no singulares.

Cabe destacar que el hecho de que una matriz cuadrada sea invertible no garantiza que todas las matrices cuadradas lo sean, ya que existen matrices que no tienen inversa.

A continuación, se explica el proceso de encontrar la matriz inversa; para esto se tomará la matriz con la cual se trabajó en el subtema anterior.

Ejemplo:

Sea

 

Una matriz aumentada; encuentra su matriz inversa mediante operaciones por renglón.

Para comenzar, únicamente se trabajará con la parte izquierda de la matriz, es decir con

A esta matriz la vas a aumentar con la matriz identidad de 3x3, de la siguiente manera:

Para encontrar la matriz inversa, lo que se tiene que hacer es realizar operaciones por renglón, hasta convertir a la matriz de la izquierda en una matriz de identidad; la matriz que se obtenga en la parte de la derecha será la matriz inversa que se está buscando.

Se realizarán los cálculos para encontrar la matriz inversa:

Entonces en el lado izquierdo de la matriz aumentada se ha generado la matriz identidad; entonces, el lado derecho representa a la matriz inversa de A, es decir:

Para comprobar que A^-1 efectivamente es la matriz inversa de B se puede realizar el producto matricial AA^-1, o bien A^-1A.