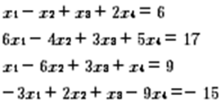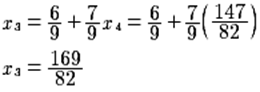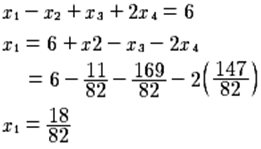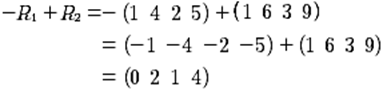En este sistema se van a desarrollar la solución de los sistemas de ecuaciones lineales utilizando matrices; se explica el procedimiento para encontrar la solución de un sistema mediante la representación matricial y el empleo de los métodos de Gauss y de Gauss-Jordan; dichos procedimientos facilitan la manera de resolver cualquier sistema de ecuaciones mediante una matriz.
Otra forma de dar solución a un sistema de ecuaciones es utilizando el determinante de una matriz asociada.
¿Sabías que…?
Se cuenta que, en la lápida de Diofanto, un gran matemático griego, podía leerse el siguiente epitafio:
“…Transeúnte, está en la tumba de Diophante: es el quien con esta sorprendente distribución te dice el número de años que vivió. Su juventud ocupo una secta parte, después durante la doceava parte su mejilla se cubrió con el primer vello. Paso una séptima parte de su vida antes de tomar esposa, y cinco años después, tuvo un precioso niño que, una vez alcanzada la mitad de la edad de su padre, pereció de una muerte desgraciada. Su padre tuvo que sobrevivirle, llorarle durante cuatro años. De todo esto, se deduce su edad.”
En su forma actual lo anterior puede representarse de una ecuación lineal…
5.1 Método de eliminación de Gauss
El método de eliminación de Gauss es el método más básico y simple que se puede utilizar para resolver un sistema de ecuaciones lineales; los elementos necesarios para desarrollarlo ya los conoces.
Básicamente, este método consiste en aplicar operaciones de renglón a una matriz hasta convertir en una matriz triangular superior, a partir de ello, se pueden encontrarlas soluciones del sistema de ecuaciones del cual procede la matriz por un método más simple; este puede ser el de inspección.
Se va a desarrollar un ejemplo para conocer el método de eliminación gaussiana o de Gauss.
Ejemplo:
Se tiene el siguiente sistema de ecuaciones lineales:
Lo primero que hacemos es construir la matriz asociada al sistema de ecuaciones lineales; esto es, la matriz principal aumentada, la cual es:
Se va a reducirla mediante operaciones por renglón, hasta obtener una matriz triangular superior, puesto en esto consiste el método de eliminación de Gauss.
Se ha llegado a la forma de Gauss; tal y como se aprecia, es una matriz triangular superior; por último, lo que se tiene que hacer es encontrar las soluciones del sistema de ecuaciones a partir de la matriz obtenida, para esto, se asocia a cada columna una variable, así, por la fila 4 y columna 5 se tiene que:
Además, se tiene por la fila 3 que:
Ello implica que:
De la fila 2 se tiene:
Y, por último, de la fila 1 se tiene:
Por tanto, las soluciones del sistema de ecuaciones son:
5.2 Método de Gauss-Jordan
El método de Gauss y el de Gauss-Jordan son muy similares; en el proceso de solución de un sistema de ecuaciones lineales es más utilizable el método de Gauss, ya que en este se hace un 50% menos de operaciones que en el método de Gauss-Jordan. El hecho de que la mayoría de las personas trabajen con este último, se debe a que permite conocer la matriz inversa proveniente de un sistema de ecuaciones lineales. Gauss-Jordan lo has utilizado anteriormente para encontrar la matriz inversa; desarrollara in ejemplo en el cual visualices y con esto compares este método con el de Gauss y establezcas el de tu preferencia.
Suponiendo que se tiene el siguiente sistema de ecuaciones:
Su matriz aumentada asociada es:
Para resolver este sistema por el método de Gauss-Jordan, lo que se debe hacer es encontrar la matriz identidad basados en la matriz A. Esto es, se aplica el método de Gauss y se encuentran los unos de la diagonal principal. Luego se convierten también en ceros los número arrida de la diagonal principal. Recuerda que ya lo habías hecho y se obtuvo la matriz:
Dada la cual, se deducen automáticamente los resultados del sistema de ecuaciones:
Con este método, como recordaras, también es posible encontrar la matriz inversa:
−1+3→3 para que el elemento a31 sea igual a cero, se multiplica el renglón 1 por -1 y se suma el renglón 3, el resultado lo vas a colocar en el renglón 3 por lo que el renglón 1 pasara tal como está.
Este resultado lo puede observar en el renglón 2 de la siguiente matriz:
El resultado lo puedes observar en el renglón 3 de la siguiente matriz.
-1/8R2—>R2 multiplicamos al renglón 2 por -1/8 para tener al 1 en la matriz principal.