Unidad 1. Operaciones con vectores

Debido a su uso, los vectores poseen ciertas propiedades que permiten sumarlos, restarlos y multiplicarlos; sin estas propiedades prácticamente serian inservibles, ya que se utilizarían únicamente como la representación de un problema sin mayor uso que eso.

Actualmente, se les de un uso similar al de los números racionales, ya que, a pesar de no poder colocar todos sus elementos, se sobreentiende la manera en que estos se extienden, por ejemplo, al colocar una serie de números: 2, 4, 6, 8, …, se entiende que se deben colocar los números pares; de manera análoga, con el uso de vectores, se puede escribir u=(2, 4, 6, 8,…) y de igual manera se entiende con este lenguaje. En el presente tema se muestran las operaciones que se pueden efectuar con los vectores, sus propiedades y algunos de sus usos.

Multiplicación de un escalar por un vector.

Para comenzar con esta sección, se utilizarán los vectores y se multiplicarán por un escalar o bien por un número.

Sea el vector V= (a, b) y sea α un número; se tiene que

Con lo que:

Esto significa que cuando un vector es multiplicado por un escalar distinto de cero, hace que la longitud de dicho vector se multiplique por el valor absoluto del escalar.

Propiedades del producto un vector por un escalar.

Cuando un vector es multiplicado por un escalar, o bien por un número, ello puede causarle un cambio de sentido o de magnitud. A continuación, se darán algunas propiedades del producto por un escalar.

Sea v y w vectores y α y β escalares; entonces, se cumplen las siguientes propiedades del producto:

αu también es un vector

Hasta el momento, únicamente se ha utilizado y comprobado la primera propiedad.

Suma de vectores.

Sea u = (a₁, a₂) y v = (b₁, b₂) dos vectores en el plano, se define la suma de dos vectores como un nuevo vector, cuyas componentes están formadas por la suma de las componentes de u y de v; el vector resultante se denota por u + v, y la suma se representa como:

Para sumar sectores en el espacio el proceso es similar, lo único que cambia es que se realiza la suma de tres coordenadas, como se muestra a continuación.

Sean:

Dos vectores; entonces la suma de ellos se representa por u + v,

Con esto ya se esta preparado para poder realizar la suma de dos vectores.

Ejemplos.

1.       Encuentra las coordenadas del vector que representa la suma de los vectores u= (3,5) y v= (-1,6)

Ahora se debe encontrar u + v, tal y como se muestra a continuación:

Observa lo que representa la suma de dos vectores en el plano:

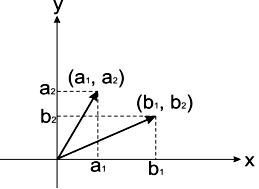
Sean = (₁,₂) y = (₁,₂); se colocan en el plano cartesiano, tal y como se muestra la figura:

Se pueden visualizar a ambos vectores como líneas que tienen un punto inicial, un punto final, una dirección y un sentido. En este caso, se toman en el primer cuadrante del plano cartesiano; de igual manera, pueden presentarse en cuadrantes distintos, ambos negativos o con signos distintos; esto no afecta el significado que tiene la suma de dos vectores desde el punto de vista geométrico.

En la figura de la izquierda, se observa el vector u + V, y en la de la derecha se puede apreciar que dicho vector representa a la diagonal de un paralelogramo que tiene por |u| y |v|.

Esta es la representación geométrica de la suma de dos vectores y se utiliza para resolver problemas tales como encontrar el área del paralelogramo formado por los vectores u y v o, para encontrar el área del del triángulo con lados u y v. Esto último también es posible con tres vectores que no sean colineales, es decir, que no se encuentren en una misma línea recta.

Resta de vectores.

La resta de vectores es muy similar a la suma; para poder obtener la resta de dos vectores, se restan las coordenadas que se encuentran en la misma posición de cada uno de los vectores; par ser explícitos, observa la siguiente representación.

Sean = (₁, ₂) y = (₁, ₂) dos vectores en el plano, encontrar la diferencia de los vectores v – u = (₁ − ₁, ₂ − ₂).

Se representan en el plano cartesiano, tal y como se muestra a continuación.

En la izquierda se encuentra la representación de los vectores y , en la derecha se muestra el vector resultante de la diferencia – .

Para entender de donde surge la diferencia, se realizarán los siguientes cálculos.

Esto significa que el vector es el vector resultante de la suma de los vectores v – u y u; dado que, u y v ya están trazados, únicamente se unen mediante otro vector; debido a que el punto final del vector resultante coincide con el punto final de la suma de los vectores, entonces v - u tiene su punto final en la punta de v y su punto inicial en la punta de u.