Los productos vectoriales tienen diversas aplicaciones, sobre todo en las ramas de la física; de igual manera, los encontraras en diferentes situaciones de tu vida.
Por ejemplo, al realizar una competencia de salto de longitud, aparentemente esta consiste en correr, saltar y caer, pero en esta actividad, también intervienen los vectores. Si todos los atletas tuvieran las mismas capacidades físicas, los vectores definirían quien sería el ganador, debido a un producto de dos vectores: uno que estaría representado por la velocidad con la que corre un atleta y el otro representado por la velocidad con la cual salta; este producto permitiría encontrar el ángulo entre los vectores ya mencionados y a partir de el, se podría encontrar en que dirección deben saltar para llegar más lejos.
Producto escalar.
Sean = (1, 1) y = (2, 2), entonces se define el producto escalar o producto punto de dos vectores ∙ como sigue:
Esto significa que el producto escalar de dos vectores da como resultado un escalar; de ahí que lleve el nombre de producto escalar.
A continuación, se realiza la representación geométrica del productos escalar de dos vectores.
Sean u y v dos vectores diferentes de cero. Entonces el ángulo entre u y v está definido como el ángulo más pequeño entre las representación de u y v que tienen el origen como punto inicial. Si u=av para algún escalar , entonces
El ángulo comprendido entre dos vectores puede presentarse de diferentes formas, tal y cono se muestra en las siguientes figuras.
En las figuras a) y b) se observa el ángulo que forman dos vectores entre sí; en c) se observa a v cuando v = u con < 0 y por último en d) se observa a = con > 0.
Ahora que ya sabes realizar el producto escalar de dos vectores, se puede demostrar el siguiente teorema:
Teorema.
Sea v un vector. Entonces
Este teorema lo puedes demostrar fácilmente como sigue:
Sea v = (a, b), entonces
Y, además,
La parte más importante del producto escalar entre dos vectores es que permite conocer el valor del ángulo que existe entre ellos, eso es lo que precisamente dice el siguiente teorema.
Teorema.
Sean u y v vectores diferentes de cero, si es el ángulo que existe entre ellos, entonces.
Con la fórmula anterior se puede encontrar el ángulo que existe entre dos vectores, a la vez que da otra manera de definir el producto escalar de u con V, despejando y quedaría como sigue:
Ejemplos.
1. Calcula el ángulo que existe entre los vectores u= 3 + 5 y = − 2. Se aplicará la fórmula para obtener el ángulo entre dos vectores como sigue:
El ángulo que hay entre u y v es de aproximadamente 122.47 grados.
Condición de perpendicularidad.
Antes de comenzar con las condiciones que deben de cumplir dos vectores para ser perpendiculares, se presentan los vectores paralelos.
Definición de vectores paralelos.
Dos vectores diferentes de cero u y v son paralelos si el ángulo que existe entre ellos es cero o .
Esta condición dice que los vectores paralelos pueden tener la misma dirección o diferente, dependiendo el valor del ángulo que entre ellos existe.
Al calcular el producto escalar de dos vectores paralelos, este se realiza de manera similar al producto de dos vectores no paralelos; el resultado del producto es lo que hace ver si dos vectores son o no paralelos.
Ejemplo.
Encuentra el producto escalar del siguiente par de vectores y establece si son o no paralelos entre sí; además, encuentra también si tienen la misma dirección o diferentes direcciones.
Realizando el producto escalar, se tiene:
Por lo tanto, los vectores son paralelos, ya que el cos = 1, únicamente cuando el ángulo es cero y como el ángulo es cero, entonces, u y v tienen la misma dirección.
Sobre los vectores paralelos, se tiene el siguiente teorema.
Teorema
Si ≠ 0, entonces = para alguna constante si y solo si u y v son paralelos.
Ahora se va a conocer el momento cuando dos vectores son perpendiculares entre sí.
Los vectores u y v diferentes de cero, son perpendiculares u ortogonales si el ángulo entre ellos es /2.
Ejemplo.
Demuestra que los vectores =+2 y = −4+2 son perpendiculares.
Primero, se obtiene el producto escalar de los vectores.
Ahora se obtiene el ángulo que existe entre ambos vectores.
Debido a que el numerador es cero, entonces
cos = 0
se tiene que el ángulo, o bien es de 90º, o de 270º, para que no existan confusiones, siempre se utilizaran ángulos que se encuentren dentro del intervalo (0º, 180º). Tomando esto en cuenta, se puede asegurar que dos vectores u y v diferentes de cero son perpendiculares, si y solo si, su producto escalar es cero.
Ahora se va a demostrar el siguiente teorema.
Teorema
Sea v un vector diferente de cero, entonces, para cualquier otro vector u distinto de cero el vector
Es un vector perpendicular a v.
Propiedades del producto escalar.
El producto escalar tiene propiedades básicas dentro del álgebra lineal, las cuales son:
Propiedad conmutativa.
Sean u y v vectores, entonces
Propiedad asociativa, respecto al producto por un escalar
Sean u y v dos vectores y sea un escalar, entonces
Propiedad distributiva respecto de la suma vectorial
Sean u, v y w vectores, entonces
Se va a demostrar la primera de las propiedades; entonces, se tiene que:
- Dado los vectores u y V, demostrar que:
Suponiendo que u= (a, b) y además que V= (c, d). Ahora,
Debido a que y , es el producto ordinario de dos números, entonces se puede utilizar la conmutatividad de la multiplicación.
Con esto se demuestra la primera propiedad del producto escalar.
Aplicaciones del producto escalar.
En este subtema se va a dar respuesta a uno de los problemas que se plantearon, con el fin de mostrar las aplicaciones que tiene el producto escalar.
El primer problema que se planteo es el siguiente:
Problema 1.
un piloto de una prestigiada aerolínea mexicana tuvo vacaciones en su trabajo y regreso con su familia a la capital mexicana; debido a que viajo por todo el mundo, traía consigo efectivo en diferentes tipos de monedas. Siendo estas: 8,500 yen, 300 libras esterlinas, 400 euros, 85 dólares, 500 soles y 200 francos. Si el tipo de cambio en moneda mexicana es de 0.16 el yen, 20.15 una libra esterlina, 16.76 un euro, 12.96 el dólar, 4.7 el sol y 13 el franco suizo.
a) Representa las cantidades en efectivo que tiene el piloto mediante un vector que representa las cantidades que tiene el piloto, entonces, se tendrá que
b) Representa el tipo de cambio de cada moneda mediante un vector. Sea v el vector que representa los tipos de cambio; entonces, siguiendo el mismo orden que u, se tiene que
c) Encuentra la cantidad total de efectivo en pesos mexicanos que tiene el piloto; para esto, utiliza el producto escalar.
Desarrollando el producto escalar de los vectores anteriores, se tiene:
Entonces el piloto tiene un total equivalente a $20,160.6
Producto cruz
Hasta este momento, se ha visto todo lo referente al producto escalar de dos sectores; a continuación, se presenta lo que corresponde al producto cruz o bien, producto vectorial, el cual está definido únicamente en ℝ3, tal y como se muestra a continuación.
Sean = 1+ 1+ 1 y = 2 + 2+ 2, el producto cruz de u y V, representa un nuevo vector que se denotara como u X v y se define por
El producto cruz es muy diferente del producto escalar de dos vectores; la diferencias más notoria, radica en que el resultado del producto escalar es una escalar y el resultado del producto cruz es un vector.
Se realizarán algunos ejemplos del producto cruz.
Sean = 3+−2 y =4−2+ dos vectores en el espacio; calcula su producto cruz.
En este caso, para calcular el producto cruz, se debe utilizar la definición que se avada de conocer e identificar los elementos de cada vector; del vector u son: 1=3, 1 = 1 y 1 = −2; por otra parte, los elementos del vector v son 2 = 4, 2 = −2 y 2 = 1; ahora, se van a sustituir estos valores, en la fórmula que define el producto cruz de ambos vectores, como sigue:
Más adelante se conocerá un método más sencillo para realizar el calculo de este tipo de productos; de momento, se resolverán mediante el uso de la definición.
Propiedades del producto de cruz.
1) ×0 = 0 × = 0
2) × = −(×)
3) ()× = ( ×).
4) ×(+) = ( ×) + ( ×)
5) ∙(×) = ∙(×) = 0.
6) × = 0, con y distintos de cero, únicamente cuando u y v son paralelos.
Estas son algunas de las propiedades del producto cruz; se realiza la demostración de las dos primeras:
1) ×0 = 0 × = 0
Sea u un vector, se va a demostrar que
Antes de comenzar con la demostración, se debe entender que el producto cruz se puede realizar únicamente entre dos vectores; así entonces, el 0 por el cual se está multiplicando u es el vector 0, el cual tiene por coordenadas 0=0i+0j+0k.
Ahora ya están listos para comenzar.
Suponiendo que = + + y ya se sabe que 0 = 0+0+0
Se identifican los valores correspondientes para aplicar la definición del producto cruz, con lo cual se tiene que 1 = , 1 = y 1 = , y a su vez, 2 = 2 = 2 = 0
Teniendo los vectoresu y 0, se define el producto cruz de ambos como:
El producto 0 × se realiza de manera análoga a la que se desarrolló; de esta manera, se demostró la primera propiedad del producto cruz.
2) × = −(×)
Se va a realizar la demostración de la segunda propiedad; para esto, sean = 1+ 1+ 1 y = 2+ 2+2; entonces se tiene
En este ultimo calculo se puede observa que los elementos de u se han cambiado con los elementos de V, así que por la definición de producto cruz, se tiene que:





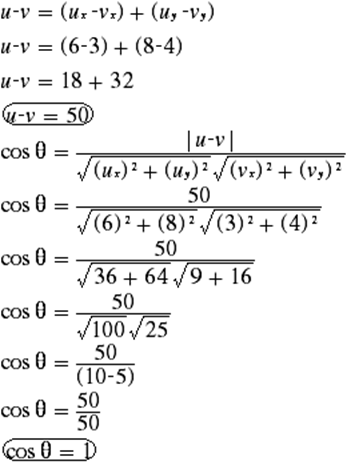
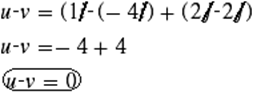





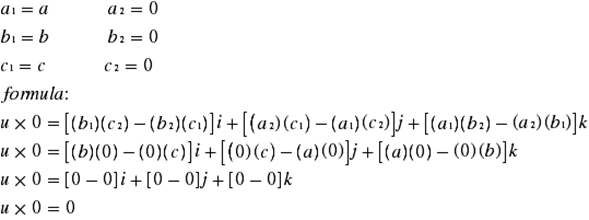

No hay comentarios.:
Publicar un comentario