En este tema se van a resolver algunos sistemas de ecuaciones lineales utilizando un método que se conoce como regla de Cramer y está basado en la obtención de ciertos menores y cofactores de algunos determinantes relacionados a matrices asociadas al sistema de ecuaciones.
La regla de Cramer da solución a un sistema de ecuaciones lineales en términos de ciertos determinantes, asociados con la matriz de dicho sistema. Recuerda que revive su nombre debido a que este método fue publicado en 1750 por el matemático Gabriel Cramer en su libro Introduction à l’analyse des lignes courbes algébriques.
Aunque la regla de Cramer es un método muy útil en la solución de ciertos sistemas de ecuaciones, su aplicación resulta ineficiente para grandes matrices, pues es sumamente laboriosa para sistemas de más de cuatro incógnitas y por ello suele no ser usado en aplicaciones que involucran muchas ecuaciones.
2.1 Regla de Cramer.
La regla de Cramer es uno de los métodos más sencillos que se utilizan para resolver un sistema ecuaciones lineales y se utiliza por medio de las matrices y sus determinantes. Además, relaciona la solución de los sistemas de ecuaciones lineales con el determinante de la matriz asociada a dicho sistema.
Ya vieron que un sistema de ecuaciones lineales puede representarse como:
Para trabajar con la regla de Cramer, a partir de una matriz A, se deben construir otras matrices, las cuales se denotarán como Ai. Cada Ai es idéntica a A, excepto por la columna i. En cada Ai la columna i será reemplazada por el vector b. De esta manera, al obtener los determinantes de cada una de las matrices formadas, se podrá aplicar la regla de Cramer.
Se representan los determinantes obtenidos de las matrices Ai como sigue.
Una vez que ya sean establecidos todos estos elementos, se puede dar a conocer la regla de Cramer, la cual establece lo siguiente:
Sea A una matriz de nxn tal que |A|≠0, entonces, el sistema Ax=b tiene como única solución a x1, x2, x3, …, xn.
Donde
Donde, Di representa el determinante de la matriz Ai y D representa el determinante de A.
Verán el siguiente ejemplo, para comprender la regla de Cramer.
Ejemplo.
Resuelve el siguiente sistema de ecuaciones utilizando la regla de Cramer.
Lo primero que deben hacer es recordar cómo se representa un sistema de ecuaciones por medio de matrices y vectores, es decir, la forma:
Para el sistema anterior se tiene que los datos correspondientes son:
Con esto, se puede representar el sistema de ecuaciones como:
Una vez que se tiene la matriz A asociada del sistema y su vector b de constantes, se pueden encontrar los elementos que se necesitan para aplicar la regla de Cramer.
Primero, se encuentran las submatrices Ai; para ello se debe reemplazar en A la columna i por b, de la siguiente manera:
A continuación, encontraran los determinantes de las submatrices anteriores.
Ahora, se encuentra el determinante de la matriz principal A.
En este momento, se tiene todos los elementos que se necesitan para aplicar la regla de Cramer, lo cual se hace a continuación.
Para una matriz de 3x3, la regla de Cramer establece que la solución de un sistema de ecuaciones lineales está dada por:
De esta manera, para el sistema de ecuaciones lineales, se tiene que la solución única es:
Como ya se había comentado, la regla de Cramer relaciona un sistema de ecuaciones con su determinante para encontrar la solución que satisface las condiciones de dicho sistema lineal.
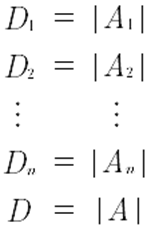
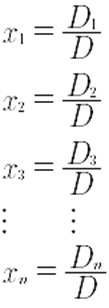

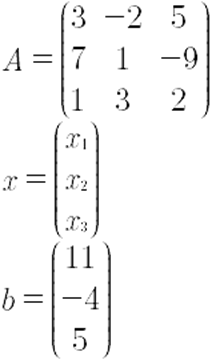
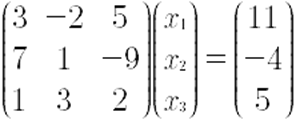
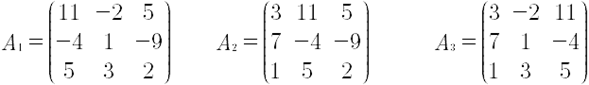
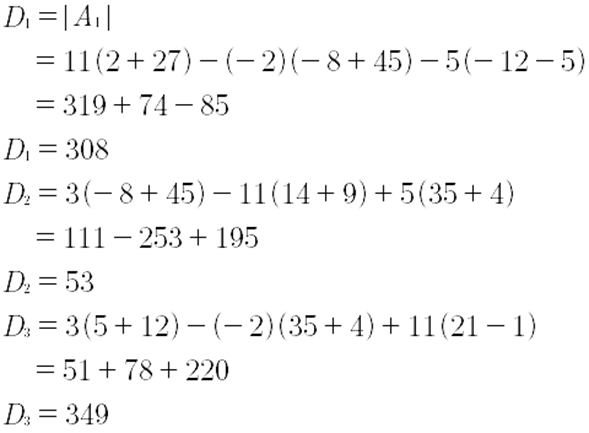
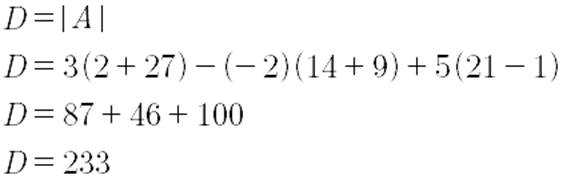
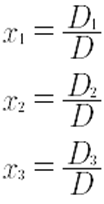
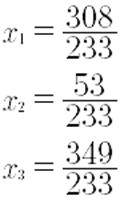
No hay comentarios.:
Publicar un comentario