De acuerdo con Deivi (2006) los inicios de la teoría de determinantes de matrices datan del siglo II a. C., con los matemáticos chinos. La idea de determinante apareció en Japón y Europa casi al mismo tiempo. En Japón, fue Takakasu Seki Kowa (1642 – 1708) el primero en publicar un trabajo sobre este tema. En 1683, Seki escribió un manuscrito titulado Método de resolver los problemas disimulados, en el cual se incluyen algunos métodos matriciales expuestos en forma de tablas.
De las primeras menciones formales que se hicieron en Europa acerca de los determinantes, aunque bajo otros nombres, se encuentra la de Cardano, quien en su Ars Magna de 1545, mostro una regla para resolver sistemas de dos ecuaciones lineales con dos incógnitas, a la cual llamo regula de modo. Esta regla forma parte de la que hoy se conoce como regla de Cramer y se aplica a sistemas de dos ecuaciones lineales con dos incógnitas.
Posteriormente, durante el año 1683, Leibniz, mediante una carta dirigida a Guillaume de L’Hospital (1661-1704), explico que cierto sistema de ecuaciones lineales tiene solución; utilizo la palabra “resultante” para ciertas sumas combinatorias de términos de un determinantes y probo varios resultados sobre estos resultantes, incluyendo uno que, en esencia se retoma en la regla de Cramer.
El matemático escoses Colin Maclaurin (1698 – 1746) utilizo determinantes en su Treatise of Geometry, para resolver sistemas de ecuaciones lineales de cuatro incógnitas. Este tratado fue publicado póstumamente en 1748. Su método fue popularizado dos años después por el matemático suizo Gabriel Cramer como Regla de Cramer, quien en 1750 la público en su Introduction à l’analyse des lignes courbes algebriques.
En esta sección se definirán los determinantes, estudiaras sus propiedades más importantes y como estas hacen más sencillo el cálculo de aquellos. También conocerás algunos conceptos relacionados, como el de menor y cofactor.
Posteriormente, revisaras como resolver sistemas de ecuaciones lineales por medio de los determinantes y finalizaras atendiendo algunos ejemplos de aplicaciones del álgebra lineal en diferentes áreas.
¿Sabías que…?
Gerolamo Cardano era médico de profesión y fue el pionero en la descripción de la fiebre tifoidea.
Cardano nació el 24 de septiembre de 1501, en Milán y murió el 21 de septiembre de 1576, en Roma. Su padre, Fazio Cardano, era abogado con una amplia experiencia en matemáticas, a tal grado que dio clases de geometría en la Universidad de Pavía, donde Leonardo da Vinci, al parecer amigo suyo, llego a consultarlo sobre algunos temas de esta área.
El joven Gerolamo aprendió matemáticas con su padre al trabajar como asistente para él. Posteriormente, se decidió a estudiar medicina y se graduó en 1525, obteniendo una excelente reputación y reconocimiento.
Según una leyenda, Cardano predijo el día de su muerte utilizando la astrología y llegado el di se suicidó para hacer correcta la predicción.
En la actualidad, Gerolamo Cardano es más conocido por sus trabajos en diversas áreas de las matemáticas, tales como álgebra y probabilidad.
3.1 Introducción a las determinantes.
Los determinantes están definidos para matrices cuadradas, es decir, de nxn. El determinante de una matriz cuadrada es un escalar (número). Se apoya en las matrices de 2x2 para describir cómo se obtienen los determinantes de matrices de orden superior.
Sea:
Se define el determinante de A y se denota por |A| como sigue:
Esta es la forma general en la que se define el determinante de una matriz de 2x2, que es el resultado de una multiplicación cruzada de los elementos de la matriz. Aquí puedes observar que el determinante de una matriz es un escalar. Dicho escalar permite obtener información sobre la matriz a partir de la cual se obtuvo; por ejemplo, el determinante de una matriz puede indicar si una matriz es invertible o no.
Para obtener el determinante de una matriz de 3x3, se utilizará la siguiente definición:
Sea la matriz A de 3x3 igual a
Entonces, se define el determinantes de A (|A|) como sigue:
Ahora, se mostrarán ejemplos de cálculo de determinantes para comprender mejor la definición.
Ejemplo.
Sea:
Calcula el determinante de A.
Para encontrar el determinante se va a utilizar la definición; en este caso, se está trabajando con un determinante de 2x2, por lo cual se utilizará la primera definición. Para ello, se debe identificar en la matriz cada elemento de la definición; los elementos son:
Una vez que se han identificado los elementos que corresponden a la definición, se desarrollara el determinante, tal y como se muestra a continuación:
Por lo tanto, el determinante de la matriz A es 7.
Ahora, se va a calcular el determinante de una matriz de 3x3.
Sea la matriz:
Calcula su determinante.
Nuevamente, se indican los elementos de la matriz que corresponden a la definición, de la siguiente manera:
Se aplica la definición y se encuentra el determinante de A, como sigue:
Se resuelven los determinantes de 2x2 para poder completar el determinante de 3x3, tal y como se muestra a continuación:
Al observa este resultado, se debe tener en cuenta que en una matriz A el símbolo |A| no significa el valor absoluto de la matriz A, ya que el valor absoluto de un número siempre es positivo y por su parte, el determinante de una matriz puede ser tanto positivo como negativo.
El método mediante el cual se resolvió el determinante es conocido como método de expansión de cofactores. Más adelante se darán los detalles de la definición de dicho método.
Para resolver una matriz de 4x4, se tienen que resolver 4 determinantes de 3x3; de la misma manera, al resolver un determinante de 5x5, se tienen que resolver 5 determinantes de 4x4 e inductivamente se desarrollan los demás determinantes, de tal manera que al realizar un determinante de nxn con n≥3 se deben de realizar n determinantes de (n-1) x (n-1).
¿Sabías que…?
Pese a que hace más de dos mil años los matemáticos chinos habían descubierto ya un método de resolución de sistemas de ecuaciones lineales equivalente al método de Gauss y por lo tanto empleaban tablas con números que actualmente se conciben como arreglos de matrices y determinantes, la aparición formal de los determinantes en las matemáticas fue hasta el siglo XVI ¡más de un siglo antes que las matrices! Cuyo tratamiento formal vio la luz hasta el siglo XIX. El término matriz fue creado por James.
3.2 Menores y cofactores de un determinante.
Sea A una matriz cuadrada de nxn y sea Mij la matriz de (n-1) x (n-1) que se obtiene eliminando A de la fila i y la columna j, a Mij se le conoce como el menor ij de la matriz A.
Al desarrollar un determinante de la matriz A de nxn con n≥3 siempre se van a encontrar con al menos 3 de los menores de A; por ejemplo, cuando se calcula el determinante de la matriz.
Se encuentran con los siguientes tres menores:
Aunque estos no son los únicos menores de A.
Debe de observarse que en una matriz de nxn con n>2, se encuentran nxn menores.
Existe un concepto muy importante dentro de las matrices, específicamente hablando de los determinantes, el cual está íntimamente ligado al concepto de menores; dicho concepto es el de cofactor, el cual tiene la siguiente definición.
3.2.1 Definición de cofactor.
Sea A una matriz de nxn. El cofactor ij de A, denotado por Aij, se obtiene de la siguiente manera:
Esto significa que el cofactor ij de A se obtiene multiplicando (-1) i+j por el determinante del menor ij.
Como puedes ver, el signo del menor se cambia si la suma i+j es impar y se conserva si es par, ya que (-1) i+j da un negativo cuando i+j es impar, y da un positivo cuando i+j es par.
Ahora, están preparados para conocer cómo se define el método de expansión por cofactores.
Sea A una matriz de nxn, entonces, para obtener el determinante de A se realizan las siguientes operaciones:
A la expresión anterior se le conoce como método de expansión por cofactores. Este método es el más utilizado en la mayoría de los textos para el cálculo del determinante de las matrices. Y aunque en algunos textos no hacen referencia a él, implícitamente lo utilizan ya que, si te fijas, utilizar los cofactores de A es igual que remitirte al determinante del menor cuando tapas la primera fila y vas recorriendo la columna.
En el cálculo del determinante de la matriz A de 3x3 del subtema anterior, se utilizaron 3 cofactores, los cuales son los siguientes:
Dichos cofactores se multiplican por los números que forman la primera fila.
Si observas, estás haciendo lo mismo que al resolver los determinantes menores.
Revisa otro ejemplo más para comprender como obtener el menor cofactor y el determinante de una matriz.
Ejemplo.
Sea la matriz
Calcula su determinante indicando los menores y cofactores que utilices para ello.
Se va a desarrollar el determinante de A, utilizando los menores y cofactores de A; para esto, primero se obtiene los menores de la siguiente manera.
Una vez que se tiene los menores se va a obtener el determinante de cada uno de ellos como sigue:
Ahora que se ha encontrado el determinante de cada uno de los menores se van a obtener los cofactores correspondientes a dichos menores, tal y como se muestra a continuación.
Una vez que se obtiene los cofactores, se aplica el método de expansión por cofactores para encontrar el determinante de A.
Primero, se coloca la ecuación para calcular el determinante de A, a partir de sus cofactores, la cual es la siguiente:
Únicamente se toman cuatro elementos debido a que A es una matriz de 4x4; la forma de expansión por cofactores se refiere a una matriz de nxn y en este caso n=4, de ahí que suceda esto.
Entonces, los elementos que hacen falta para aplicar la fórmula anterior son:
Ahora que se tienen todos los elementos se aplica la fórmula de expansión por cofactores de la siguiente manera:
Advierte que mientras mayor es la matriz, mayor es el número de operaciones que tienes que realizar para encontrar su determinante; en este caso, se calculó a partir de los menores que se obtuvieron utilizando la primera fila; debes tener en cuenta que los menores se pueden obtener utilizando cualquier fila o cualquier columna de una matriz; quizás los cálculos sean diferentes, pero el resultado final siempre será el mismo.
Esto significa que puedes obtener el determinante a partir de cualquier fila o columna de la matriz y no necesariamente a partir de la primera fila, como se desarrolló aquí.
3.3 Propiedades de los determinantes.
Existen diferentes situaciones por las cuales muy a menudo pasan, por ejemplo, si tuvieran que subir a un edificio de 4 pisos, simplemente utilizando las escalares. Sin embargo, si tuvieran que subir a la azotea de un edificio de 70 pisos, subir por la escaleras será algo demasiado agotador y causaría una gran pérdida de tiempo. Por esta razón, la gente prefiere utilizar un elevador para estos casos, ya que eso facilita el trabajo de la subida.
De la misma manera ocurre con los determinantes; como ya se percataron, realizar un determinante de 3x3 implica una gran cantidad de operaciones, realizar un determinante de 4x4 requiere al menos el cuádruple de las operaciones que se usaron para obtener un determinante de 3x3 ¡imagina si quisieras obtener un determinante de 30x30! Serían necesarios varios días para realizarlo. Además, en caso de un error en algún calculo, habría que volver a realizar las operaciones en más de una ocasión; para esos casos, se pueden ayudar con las propiedades que poseen los determinantes, lo cual se presenta a continuación.
Las propiedades de los determinantes se utilizan para facilitar su cálculo y minimizando el trabajo a realizar para obtenerlo.
Se tienen las siguientes propiedades de estos:
Propiedad 1.
Sea A una matriz de nxn; si A tiene una fila o una columna de ceros, entonces |A|=0.
Para ejemplificar esta propiedad se va a desarrollar el siguiente determinante.
Sea la matriz:
Calcula su determinante.
De entrada, por la propiedad anterior, se debe que el determinante de esta matriz es cero. Para probar como se va a desarrollar por medio de la expansión de cofactores como sigue.
Se encuentra la determinante de los menores; en esta ocasión utilizando la fila 3, de la siguiente manera:
A continuación, se calculan los respectivos cofactores, los cuales son los siguientes:
Ahora se toman los elementos de la tercera fila de A para desarrollar la expansión por cofactores, los cuales son los números cero.
Finalmente, se calcula el determinante de A tal y como se muestra a continuación:
De igual manera, se utilizará cualquier otra fila o columna de A, se obtendría de nueva cuenta el mismo resultado. A su vez, si A tuviera cualquier otra fila o cualquier otra columna completa de ceros, su determinante sería cero. Lo único que se requeriría hacer es tomar dicha fila o columna de ceros, como en este caso.
Propiedad 2.
Sea A una matriz de nxn; si se multiplica a una fila o columna de A por un escalar c, entonces el determinante de A se multiplicaría por c.
Para comprender esta propiedad, se tiene el siguiente ejemplo.
Sea:
Se van a comparar los determinantes de la matriz A y de la matriz B, donde B es la matriz que se obtiene de multiplicar la segunda columna de A por 3, dicho de otra manera.
Ahora que conoces el método de expansión por cofactores, queda a tu disposición la mejor manera para reducir tus operaciones. De ahora en adelante se realizará sin explicaciones detalladas y con la reducción de operaciones, tal y como sigue.
Mientras que:
Al comparar los determinantes de A y B y por la propiedad anterior, se tiene que se debe de cumplir que el determinante de B sea igual a tres veces el determinante de A, es decir,
Lo anterior quiere decir que, si se sustituye el valor del determinante de A y el de B en la ecuación anterior, se debe de llegar a una identidad; se hacen las sustituciones correspondientes para verificar tal identidad:
Tal y como se esperaba, se llegó a una identidad, lo cual da una idea de cómo comprobar la segunda propiedad de los determinantes, la idea de esta propiedad no es la de crear una matriz con valores más grandes, sino encontrar algún divisor de la matriz que permita hacer más pequeños a los elementos de esta.
Si observas, lo que se hizo fue obtener los determinantes a partir de la columna que se multiplico por tres. Esto es como multiplicar cada menor de A por 3, dándote una idea de que es lo que sucede en un caso general.
Propiedad 3.
Sea A, B y C tres matrices con las mismas dimensiones. Si A, B y C son iguales excepto por una columna, o fila y dicha columna o fila, en C es la suma de las mismas columnas, o fiales en A y B, entonces:
Dicho de otra manera, si la columna o fila j de C es la suma de la columna o fila, j de A es la columna o fila j de B, entonces el determinante de C es la suma de las determinantes de A y B, siempre y cuando las demás columnas o filas, de las tres matrices sean idénticas.
Se va a realizar un ejemplo de esta propiedad para observar la ayuda en cuanto a ahorro de tiempo y de operaciones que permite el utilizarla, cuando se cumplen las condiciones necesarias para su aplicación.
Sea A y B dos matrices, donde:
Calcula la suma del determinante de A con el determinante de B.
Para encontrar la suma de los determinantes, primeramente, se tiene que calcular el determinante de cada una de las matrices, tal y como sigue:
Se tiene entonces que la suma de los determinantes de A y B está dada por
Debido a que las operaciones fueron simplificadas, no se distingue la gran cantidad de operaciones que se realizaron para encontrar esta suma. Sin embargo, aun cuando la suma anterior puede verse mucho más simple si se aplica la propiedad 3 de los determinantes, para esto, lo que se hace es por inspección distinguir dos filas o columnas de A y B que sean idénticas, si existen; entonces, se forma una nueva matriz con estas dos filas o columnas y a continuación se construye la que haga falta por medio de la suma de la fila o columna de A y B que son distintas; aplicando esto, se puede construir para este ejemplo la siguiente matriz:
De la cual, al obtener su determinante, este debe ser igual a la suma de los determinantes de A y B.
Tal y como puede observarse, el proceso de obtener la suma de los determinantes de dos o más matrices puede simplificarse, siempre y cuando las matrices que se utilizan cumplan las condiciones que pide la propiedad 3; de ser así, permiten un ahorro de tiempo y esfuerzo.
Si te des cuenta, lo que se hizo fue obtener los determinantes a partir de la columna que era diferente. Por ello, todos los menores quedaron igual y lo que variaba era el número por el cual se iban multiplicando los menores. Así la obtención del determinante de la matriz C es como sumas las entradas de la columna diferentes para A y B y multiplicarlas por el menor, el cual no cambia. Esto debe darte una idea de que es lo que sucede en un caso general.
Propiedad 4.
Si A es una matriz de nxn, al intercambiar dos filas o columnas distintas de A, su determinante cambia de signo.
Uno de los usos que se le puede dar a esta propiedad es el de establecer un saldo en contra, ya sea en cuanto a capital o en cuanto a materia prima.
Se va a realizar el siguiente ejemplo, para dar uso a esta propiedad.
Sea A y B dos matrices de 3x3, donde:
Encuentra los determinantes de A y de B y comparalos.
Los primero que se hace es calcular el determinante de A y el de B:
Advierte que, las matrices A y B son idénticas, con la diferencia de que la primera y segunda columnas están intercambiadas entre una y otra matriz; debido a esto, el signo del determinante de las matrices es distinto.
Como podrás darte cuenta, lo que se hizo fue obtener los determinantes a partir de la fila que permaneció estable. Como las otras filas se intercambiaron, resulto que todos los menores quedaron iguales en cuanto a sus cantidades, pero con signos contrarios. Por ello, los determinantes son iguales en valor absoluto, pero tiene signos contrarios. Este debe darte una idea de que es lo que sucede en un caso general.
Propiedad 5.
Sea A una matriz de nxn; si A tiene dos filas o columnas iguales, entonces su determinante es cero.
Cuando se encuentra la inversa de una matriz que posea dos filas o columnas iguales, se identifica al instante que su determinante es cero; gracias a esta propiedad, se puede establecer de inmediato que dicha matriz no es invertible, por lo cual no tiene inversa.
Observen el siguiente ejemplo.
Sea A una matriz de 3x3, donde:
El valor de los elementos de A es más grande de los que comúnmente sea realizado hasta el momento; van a resolver esta matriz como en los ejemplos anteriores, aplicando la expansión por cofactores; obviamente por la propiedad que se acaba de enunciar el determinante de esta matriz es cero.
Ahora se van a desarrollar el determinante de A como sigue:
Noten la diferencia que existe entre utilizar la propiedad 4 y calcular el determinante de A por medio de la expansión por cofactores; obviamente es mucho más rápido decir que el determinante es cero por medio de la propiedad que descubrirlo por medio de las operaciones. Este ejemplo visualiza el hecho de que se simplifica el obtener un determinante si dos columnas o filas de una matriz son iguales.
Si prestas atención, lo que se hizo fue obtener el determinante a partir de la fila que era diferente. Como las otras dos filas eran iguales, y los menores se obtienen multiplicando cruzado, entonces se obtienen cantidades absolutamente iguales, pero con signos contrarios. Por ello, todos los menores quedaron iguales a cero. Para obtener el determinante de una matriz de dimensión mayor a 3x3 se van utilizando los renglones o las columnas que sean distintas. Al final se llega a las columnas o filas iguales. Esos menores dan cero, y como multiplican otros números, entonces los resultados van dando ceros. Esto debe darte una idea de que es lo que sucede en un caso general.
Propiedad 6.
Sea A una matriz de nxn; si una fila o columna de A es un múltiplo escalar de otra fila o columna, entonces, el determinante de A es cero.
Esta propiedad, al igual que la anterior, permite hacer un total de cero operaciones para encontrar el determinante de una matriz que cumpla con las condiciones para su aplicación; al respecto se tiene el siguiente ejemplo:
Sea A una matriz de 3x3, donde
Puedes apreciar que la columna 2 multiplicada por 3 es igual a la columna 3. Calcula la determinante de A.
El determinante de A es igual a:
Las operaciones efectuadas no fueron demasiadas debido a que se trataba de un determinante de 3x3, pero, aun así, se pueden resumir a nada; esto se logra analizando los elementos de la matriz. Si te percatas, existe un parecido entre las columnas 2 y 3, como ya se observaron; la columna 3 resulta de multiplicar a la columna 2 por 3, lo cual hace que A cumpla con las condiciones necesarias para aplicar las propiedades 1 y 5 e identificar de inmediato que el determinante de A es cero.
Si observas, lo que se hizo fue obtener el determinante a partir de la columna que no era múltiplo. Como las otras dos columnas era un múltiplo de la otra, y los menores se obtienen multiplicando cruzado, entonces se obtienen cantidades absolutamente iguales, pero con signos contrarios. Por ello, todos los menores quedaron iguales a cero. Para obtener el determinante de una matriz de dimensión mayor a 3x3 se van utilizando los renglones o las columnas que no sean múltiplos. Esos menores dan cero, y como multiplican otros números, entonces los resultados van dando ceros. Esto debe darte una idea de que es lo que sucede en un caso general.
Propiedad 7.
Sea A una matriz de nxn. Si se realiza la suma de un múltiplo escalar de una fila o columna de A con otra fila o columna de A, entonces el determinante de A se conserva.
Lo que dice esta propiedad es que si se hace el producto de un escalar por una fila o columna de una matriz y el resultado lo suman a otra fila o columna de la misma matriz, entonces el determinante se mantiene igual, es decir, no cambia.
Vean el siguiente ejemplo para comprender más a fondo esta propiedad. Sea A una matriz de 3x3 donde:
Y sea B la matriz que resulta de sumar a la fila 2 el triple de la fila 3, es decir,
Calcula los determinantes de A y B y comparalos entre sí.
Entonces, se calcula el determinante de A y de B como sigue:
Como puedes ver, los determinantes de ambas matrices son iguales, de lo cual se infiere que la propiedad 7 si se cumple para los determinantes de las matrices dadas.
Esta última propiedad puede utilizarse para aquellos casos en los cuales por medio de una operación con renglones se puede simplificar la matriz y con ello el cálculo de su determinante; de esta manera, se ahorra tiempo y operaciones.
Si bien aprecias lo anterior, lo que se hizo fue obtener el determinante a partir de la fila que sufrió los cambios. Como las otras dos filas no se alteran, los menores permanecen iguales en ambas matrices. Así, lo que se altera es el renglón de los números que van a multiplicar a los cofactores. Pero como se obtiene estos multiplicando por el mismo escalar y sumando los correspondientes números del otro renglón. Entonces lo que se aumenta en una parte se quita en la otra. ¿lo observaste? Esto debe darte una idea de que es lo que sucede en un caso general.
¿sabías que…?
Algunos de los más grandes matemáticos de los siglos XVIII y XIX contribuyeron al desarrollo de las propiedades de los determinantes. La mayoría de los historiadores coinciden en afirmar que la teoría de los determinantes se originó con el matemático alemán Goofried Wilhelm Leibniz (1646 – 1716) quien fue con Newton, el coinventor del cálculo diferencial e integral. Leibniz empleo los determinantes en 1693 en relación con los sistemas de ecuaciones lineales simultaneas. No obstante, hay quienes creen que el matemático japonés Seki Kowa hizo lo mismo unos 10 años antes.
En 1858, el matemático inglés Arthur Cayley publicó unas “Memorias sobre la teoría de matrices” en la que daba la definición de matriz y las operaciones suma de matrices, de producto de un número real por una matriz, de producto de matrices y de inversa de una matriz. Cayley afirma que obtuvo la idea de matriz a través de la de determinante y también como una forma conveniente de expresar transformaciones geométricas.




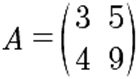





![clip_image015[1] clip_image015[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEixZC_89JJFSWxgFY4vExS5mPH6PY1Xj-WYHt-2ZJ5FaOhcT8kWWXbCAL9gb8apXB-EjjS9BqWzc7AIYUCmjSzaEw5NLtQMwAiQo9JjYzhUE5OrAV3JzMIKR9frrOFK2ADK0ebHianpQ9Br/?imgmax=800)


![clip_image019[1] clip_image019[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh8K3mBZx7D4ctnLZZFYang4oTdtJTG9p1vK8lCqhiRFaJWzD0G21CklTdodRHDf9Nn4Ke017WYokY4x_QrJPagS49LIGARRNwhe7JJ7xl07vRbjWFnZexgUFeMgGqiYbSNFD4Pu4LgBcE7/?imgmax=800)



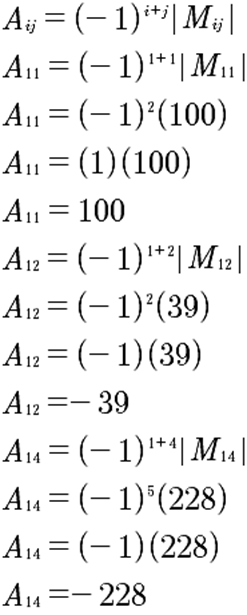







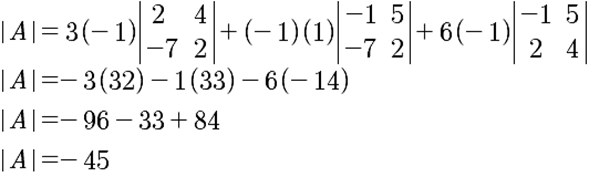
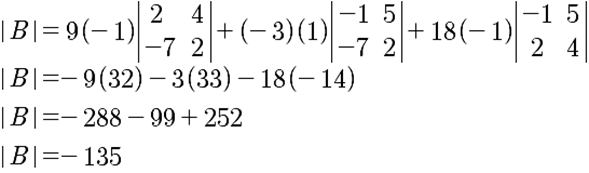







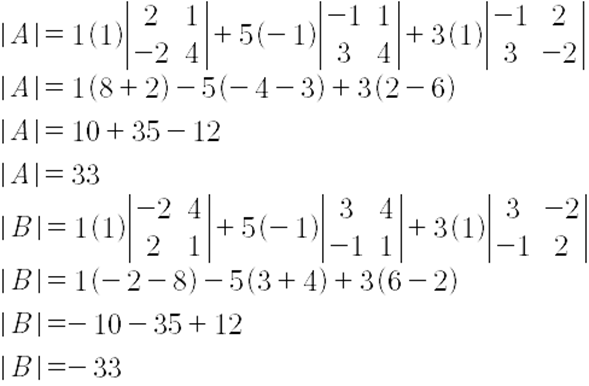


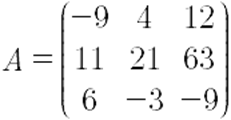




No hay comentarios.:
Publicar un comentario