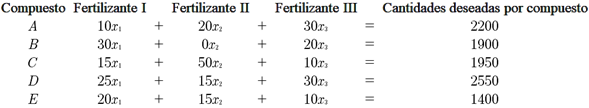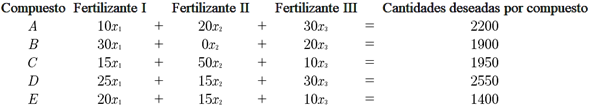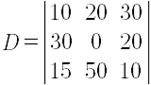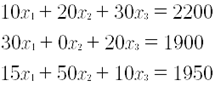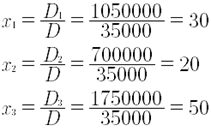El álgebra lineal tiene una gran cantidad de aplicaciones en muchos campos del conocimiento humano, tanto en ciencias sociales como en ingenierías y en las llamadas ciencias exactas. El objetivo del siguiente tema es, justamente, mostrar esa utilidad del álgebra lineal.
Esto se logrará a través del desarrollo de algunos ejemplos de aplicaciones de matrices y de determinantes. Recuerda que uno de los pilares de las matrices son los vectores. A su vez las matrices dan pie al estudio de los determinantes. De esta manera, a través de los ejemplos que aquí se estudian, podrás ver también como se interactúan y se complementan todos los temas que viste en esta asignatura.
3.1 Aplicación de matrices.
A continuación, se presentan algunas aplicaciones de matrices.
Ejemplos: gráficos de computador.
El diseño asistido por computador (CAD) le ahorra a la Ford Motor Company millones de dólares cada año. Adoptados por primera vez por Ford a principios de 1970, CAD y CAM (fabricación asistida por computador) han revolucionado la industria automovilística. Hoy día, los gráficos por computador constituyen el corazón y el álgebra lineal el alma del diseño moderno de automóviles.
Muchos meses antes de que se construya un nuevo modelo de automóvil, los ingenieros diseñan y construyen un automóvil matemático: un modelo de alambre que existe solamente en la memoria de un computador y en las terminales de exhibición de gráficos. Este modelo matemático organiza e influye en cada paso del diseño y fabricación del automóvil.
Trabajando en más de 2600 estaciones de trabajo para gráficos, los ingenieros de Ford perfeccionan el diseño original, esculpen las líneas fluidas de la carrocería, ponen a prueba la capacidad de las láminas de metal para soportar las deformidades y los dobleces necesarios para producir la carrocería, ajustan la colocación de los asientos interiores, planean y disponen las partes mecánicas, y producen los planos de ingeniería para los miles de componentes que los proveedores fabricaran. Los ingenieros inclusive hacen pruebas de carretera para la suspensión del carro matemático, colocan el automóvil en un túnel de viento matemático y ¡hacen repetidas pruebas de colisión del auto en el computador!
El modelo de alambre del automóvil se almacena en muchas matrices de datos para cada componente principal. Cada columna de una matriz enumera las coordenadas de un punto sobre la superficie del componente. Las demás columnas describen cuales puntos se deben conectar con curvas; un escáner tridimensional genera los puntos de datos originales pasando sensores por un modelo de arcilla de tamaño natural del automóvil. Las piezas individuales del interior también se almacenan como matrices de datos. Los componentes más pequeños se trazan con software de gráficos por computador en la pantalla y las piezas mayores se forman ensamblando matemáticamente los componentes más pequeños.
Posteriormente, los programas matemáticos generan más puntos, curvas y datos de color para interpretar y dibujar la superficie exterior del automóvil, haciendo que este se vea tan real en la pantalla que parezca un automóvil de verdad en la sala de exhibición de un distribuidor. Los clientes potenciales opinan mientras el automóvil gira en el “piso de la sala de exhibición”. Si a los clientes no les gusta, el diseño puede cambiarse antes de que se construya el coche real.
Ya sea que trabajen en el diseño general de la carrocería o modifiquen un componente pequeño, los ingenieros llevan a cabo varias operaciones básicas sobre imágenes gráficas, como cambiar la orientación o la escala de una figura, hacer un acercamiento de alguna región pequeña o cambiar entre vistas bidimensional y tridimensional. El álgebra lineal es en verdad el “alma” del software de gráficos porque todas las manipulaciones de imágenes en la pantalla se logran mediante técnicas de álgebra lineal.
|
1 Modelo de alambre de un auto |
2 Carro en un túnel de viento matemático. |
Se ha visto que los determinantes están estrechamente ligados con las matrices. Por ello, casi cualquier problema que pueda ser resuelto mediante matrices podrá ser resuelto mediante determinantes.
Ahora se resolverá un ejercicio.
Ejercicio: fertilizantes básicos.
Un grupo de ingenieros de varias áreas está analizando cinco compuestos que forman tres tipos de fertilizantes básicos I, II y III. Las cantidades se miden en gramos. Pueden obtenerse fertilizantes especiales resolviendo combinaciones de los tres tipos básicos. Es decir, los fertilizantes especiales pertenecen al espacio generado por los tres vectores que representan los fertilizantes básicos. El objetivo del estudio es crear nuevos fertilizantes que dañen menos el ambiente y el suelo.
Las cantidades de cada compuesto que forman cada uno de los fertilizantes básicos están dado en gramos y se expresan por la siguiente matriz.
Los ingenieros desean obtener un fertilizante con las siguientes cantidades:
2,200 gramos del compuesto A; 1,900 del compuesto B; 1950 del compuesto C;2550 del compuesto D y 1400 del compuesto E.
Si esto es posible, ¿Qué cantidad de cada fertilizante básico se necesitaría para formar el fertilizante especial?
Se llamará X1, X2 y X3 a las cantidades que se utilizaran de los fertilizantes básicos I, II y III, respectivamente.
Se construye el sistema de ecuaciones a partir de los datos dados y de lo que se desea obtener:
Se utilizarán X1, X2 y X3 gramos de los fertilizantes básicos I, II y III respectivamente, por compuesto A, B, C, D y E, para obtener las cantidades deseadas de cada uno en la mezcla:
Se obtiene la matriz ampliada asociada al sistema:
La matriz no es una matriz cuadrada, ya que está asociada a un sistema de cinco ecuaciones con tres incógnitas. Vean que sucede al aplicar el método de Gauss.
Se realizan operaciones sobre la matriz:
Por lo tanto, según el método de Gauss, x3 es siempre igual a 50, de donde se deduce que el sistema si tienen solución y esta es única. Si los valores asociados a x3 hubieran resultado diferentes para las filas 3, 4 y 5, el sistema no tendría solución.
Estos valores cumplen el sistema formado por las tres primeras ecuaciones. Ahora bien, si fuera posible realizar el fertilizante con las cantidades deseadas de los compuestos, se requiere que estas soluciones satisfagan también las dos ecuaciones restantes.
Por lo tanto, es posible realizar el fertilizante con una mezcla de las cantidades deseadas de cada compuesto, a partir de los fertilizantes básicos. Para ello se deben utilizar: 30 gramos del fertilizante I, 20 gramos del fertilizante II y 50 gramos del fertilizante III.
3.2 Aplicación de sistemas de ecuaciones.
A continuación, se presentan algunas aplicaciones de determinantes.
Ejemplo: modelos lineales en economía e ingeniería.
Era el final del verano de 1949. El profesor de Harvard, Wassily Leontief, estaba introduciendo cuidadosamente la última de sus tarjetas perforadas en el computador Mark II de la universidad. Las tarjetas contenían información sobre la economía de Estados Unidos y representaban un total de más de 250,000 piezas de información producidas por la Agencia de Estadísticas del Trabajo de E.U.A. tras dos años de intensa labor. Leontief había dividido la economía estadounidense en 500 “sectores”, tales como la industria del carbón, la industria automovilística, comunicaciones y así sucesivamente.
Para cada sector, había elaborado una ecuación lineal que describía como este distribuía sus salidas hacia otros sectores de la economía. Debido a que el Mark II, uno de dos computadores más grandes de aquella época, no podía manejar los sistemas resultantes de 500 ecuaciones con 500 incógnitas. Leontief destilo el problema a un sistema de 42 ecuaciones con 42 incógnitas.
Programar el computador Mark II para las 42 ecuaciones de Leontief había requerido varios meses de esfuerzo y él estaba ansioso por ver cuánto le llevaría al computador resolver el problema. El Mark II zumbo y parpadeo durante 56 horas antes de producir finalmente una solución.
Leontief, quien obtuvo el premio Nobel de Economía 1973, abrió la puerta a una nueva era en modelos matemáticos en economía. Sus esfuerzos en Harvard en 1949 marcaron uno de los primeros usos significativos de los computadores para analizar lo que entonces era un modelo matemático a gran escala. Desde ese tiempo, los investigadores en muchos otros campos han usado computadores para analizar modelos matemáticos.
Debido a las cantidades masivas de datos implicados, los modelos generalmente son lineales; esto es, se escriben como sistemas de ecuaciones lineales.
La importancia del álgebra lineal para las aplicaciones se elevado en proporción directa al incremento en la potencia del cómputo. Con cada nueva generación de hardware y software se dispara una demanda de mayor capacidad. La ciencia de computo esta así intrincadamente ligada al álgebra lineal, a través del crecimiento explosivo del procesamiento en paralelo y los cálculos en gran escala.
Los científicos e ingenieros trabajan ahora en problemas mucho más complejos que los que podían imaginarse hace algunas décadas. ¡Hoy, el álgebra lineal tiene más valor potencial para los estudiantes en muchos campos científicos y de negocios que cualquier otra materia de matemáticas de licenciatura!
· Prospección petrolera. Cuando un barco busca depósitos petrolíferos mar adentro, sus computadores resuelven miles de sistemas de ecuaciones lineales independientes diariamente. Los datos sísmicos para las ecuaciones se obtienen de ondas de choque bajo el agua producidas por medio de explosiones con cañones de aire. Las ondas rebotan en rocas bajo la superficie y se miden con geófonos sujetos a cables de una milla de largo tras del barco.
· Programación lineal. Hoy en día muchas decisiones gerenciales importantes se toman con base en modelos de programación lineal que utilizan cientos de variables. La industria de aviación, por ejemplo, usa programas lineales que organizan las tripulaciones para los vuelos, registran la ubicación del aparato organizan las tripulaciones para los vuelos, registran la ubicación del aparato aéreo o planean diversos programas de servicios de apoyo tales como el mantenimiento y las operaciones de terminal.
· Redes eléctricas. los ingenieros utilizan un software de simulación para diseñar circuitos eléctricos y microchips que incluyen millones de transistores. El software depende de técnicas de álgebra lineal y de sistemas de ecuaciones lineales.
Los sistemas de ecuaciones lineales están el corazón del álgebra lineal.
Ahora se retoma el problema de fertilizantes básicos de la sección anterior, para resolverlo por el método de determinantes.
Se había construido el siguiente sistema de ecuaciones:
La matriz asociada al sistema está dada por:
Vean que esta matriz no es cuadrada, ya que surge de un sistema de cinco ecuaciones con tres incógnitas.
Como solo pueden sacarse determinantes de matrices cuadradas, entonces se debe hacer cuadrada la matriz asociada. Para ello, se trabajará entonces solo con tres incógnitas y tres ecuaciones, es decir, se eliminarán las dos últimas filas del sistema para obtener la matriz:
Ahora sí, se puede obtener el determinante de dicha matriz:
Este es el determinante del sistema formado por las tres primeras ecuaciones:
Entonces:
Obsérvese que se sacó el determinante a partir de la segunda fila, ya que el cero simplifica las operaciones.
Ahora se sacan los determinantes asociados a las variables. Recuérdese que las entradas asociadas a cada variable son sustituidas por las entradas de las constantes:
Asociados a x1, x2 y x3 respectivamente.
Así, se sacan los valores de x1, x2 y x3 a partir de las correspondientes divisiones:
Los resultados, efectivamente, son los valores de x1, x2 y x3 que se obtuvieron a partir del método de Gauss. Ahora bien, si no se supieran los valores de x1, x2 y x3, entonces se tendrían que aplicar los valores obtenidos a las ecuaciones que no intervinieron en los determinantes, para comprobar que efectivamente esas soluciones satisfacen las dos ecuaciones restantes.